Evenly Distributing Points on a Sphere with the Golden Ratio

Recently, I watching Yuri's stream about create a sphere with points in Threejs. So I decided to write a post about it, explaining how to distribute points evenly in a sphere.

The Golden Ratio: Nature’s Secret Weapon

The golden ratio, approximately 1.618, is the irrational number (1 + √5) / 2. It’s famous in art and nature for creating balanced, harmonious proportions. Here, we use its irrationality to our advantage: it helps us avoid repeating patterns, ensuring points spread out uniformly across the sphere’s surface.

Spherical coordinates overview

In 3D space, spherical coordinates offer a way to define a point using:

• Radius: The distance from the origin (assumed to be 1 here, as it’s a unit sphere).
• Phi (φ): The polar angle, measured from the vertical axis (like colatitude, from the north pole down).
• Theta (θ): The azimuthal angle, measured in the horizontal plane (like longitude on Earth).

These angles are used to compute the Cartesian coordinates (x, y, z) of the point on the sphere.

• x = cos(θ) * sin(φ)
• y = cos(φ)
• z = sin(θ) * sin(φ)

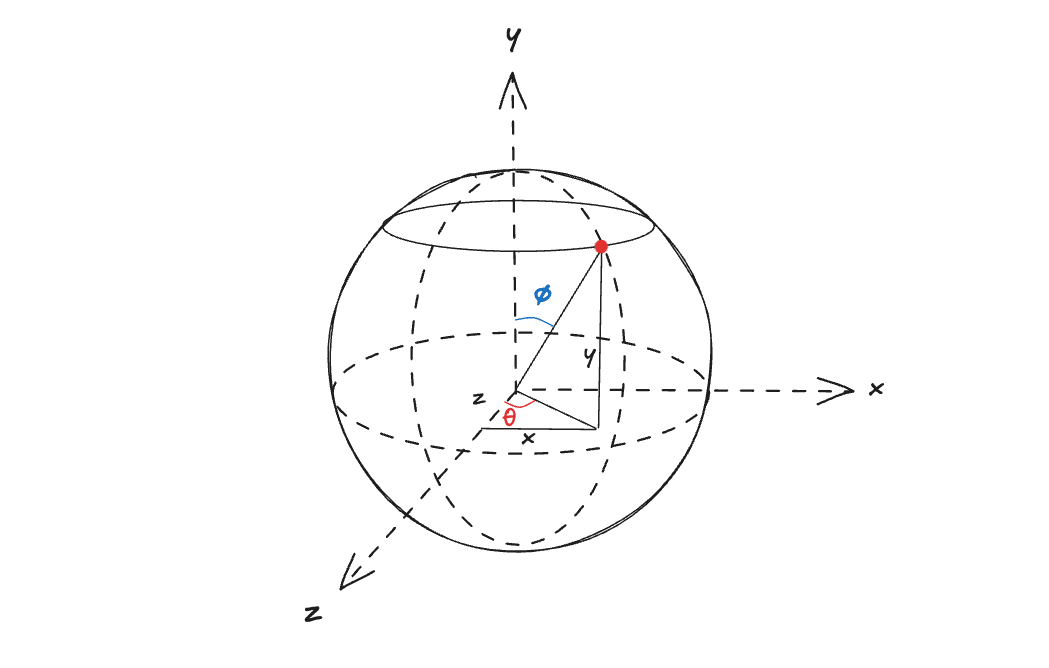
This convention aligns with a common spherical coordinate system where phi (φ) is the angle from the positive y-axis (0 at the north pole, π at the south pole), and theta (θ) is the angle in the xz-plane from the positive x-axis (0 to 2π around the equator).

Phi (φ): Polar angle, spacing points vertically

Assumed we have total 3000 points in the sphere. We can calculate the phi angle by the following formula:

const pointsNumber = 3000;

for (let i = 0; i < pointsNumber; i++) {
  const prog = i / pointsNumber;
  const phi = Math.acos(1 - 2 * prog);
}

• Progress
  • prog starts at 0 / 3000 = 0 and ends at 2999 / 3000 ≈ 0.9997. It’s a fraction showing how far we are through the points.
• Inside the Arccosine:
  • 1 - 2 * prog takes that fraction and stretches it.
  • At i = 0: 1 - 2 * 0 = 1.
  • At i = 2999: 1 - 2 * 0.9997 ≈ -0.9994.
  • This gives us a range from 1 down to almost -1.
• Calculate phi angle:
  • Math.acos (arccosine) turns that range into angles.
  • Math.acos(1) = 0 (top of the sphere).
  • Math.acos(-0.9994) ≈ 3.1396, close to π ≈ 3.1416 (bottom of the sphere).
  • So, phi goes from 0 to nearly π over 3000 steps.

Theta (θ): Azimuthal angle, spinning around the sphere

Now, theta handles the angle around the sphere at each height.

const pointsNumber = 3000;
const goldenRatio = (1 + Math.sqrt(5)) / 2;

for (let i = 0; i < pointsNumber; i++) {
  const prog = i / pointsNumber;
  const phi = Math.acos(1 - 2 * prog);
  const theta = (2 * Math.PI * i) / goldenRatio;
}

• Golden ratio: goldenRatio = (1 + √5) / 2 ≈ 1.618.

• Full circle: 2 * Math.PI is one full circle in radians.

• The angular step:

  • 2 * Math.PI / goldenRatio ≈ 3.8832 radians is the step size each time i increases

• Wrapping Around:

  • theta grows with each step, wrapping around every 2π since sin and cos repeat.
  • The irrational step ensures no exact repeats, filling the circle evenly over 3000 points.

Combining phi and theta

Now, we can calculate the Cartesian coordinates (x, y, z) of the point on the sphere.

const pointsNumber = 3000;
const goldenRatio = (1 + Math.sqrt(5)) / 2;
const positions: number[][] = [];

for (let i = 0; i < pointsNumber; i++) {
  const prog = i / pointsNumber;
  const phi = Math.acos(1 - 2 * prog);
  const theta = (2 * Math.PI * i) / goldenRatio;

  const x = Math.cos(theta) * Math.sin(phi);
  const y = Math.cos(phi);
  const z = Math.sin(theta) * Math.sin(phi);
  positions.push([x, y, z]);
}

Visualizing It

I used InstancedMesh with tiny planes (0.01x0.01) to render the points. You can see the full code below:

import { Base } from "./base.ts";
import * as THREE from "three/webgpu";
import { OrbitControls } from "three/examples/jsm/Addons.js";

class App extends Base {
  constructor() {
    super();

    const pointsNumber = 3000;
    const goldenRatio = (1 + Math.sqrt(5)) / 2;
    const positions: number[][] = [];
    
    for (let i = 0; i < pointsNumber; i++) {
      const prog = i / pointsNumber;
      const theta = (2 * Math.PI * i) / goldenRatio;
      const phi = Math.acos(1 - 2 * prog);
      const x = Math.cos(theta) * Math.sin(phi);
      const z = Math.sin(theta) * Math.sin(phi);
      const y = Math.cos(phi);
      
      positions.push([x, y, z]);
    }
        
    const dotMat = new THREE.MeshBasicNodeMaterial({
      color: new THREE.Color("#78A0F7")
    });
    
    const dotGeo = new THREE.PlaneGeometry(0.01, 0.01);

    const dots = new THREE.InstancedMesh(dotGeo, dotMat, pointsNumber);
    const obj = new THREE.Object3D();

    for (let i = 0; i < positions.length; i++) {
      const pos = new THREE.Vector3(
      	positions[i][0],
      	positions[i][1],
      	positions[i][2],
      );
      
      obj.position.copy(pos);
      obj.lookAt(pos.multiplyScalar(2));
      obj.updateMatrix();
      dots.setMatrixAt(i, obj.matrix);
    }

    dots.instanceMatrix.needsUpdate = true;
    this.scene.add(dots);
  }

  public animate() {
    this.renderer.render( this.scene, this.camera );
  }
}

new App();

Wrap Up

The golden ratio method is a neat mix of math and nature. Phi handles the vertical march, theta the circular dance, and Three.js brings it to life. And that’s how you create a sphere with points in Three.js!